(OBM 2003 – 1ª Fase – Nível 1)
Um troféu formado por cinco recipientes cúbicos foi construído da seguinte maneira: sob o cubo de lado 10 cm foi soldado o cubo de lado 20 cm, sob este foi soldado o cubo de lado 30 cm, e assim por diante. Toda a superfície externa desse troféu deverá ser coberta com um certo tipo de revestimento. Quantos metros quadrados desse revestimento serão necessários?

A) 1,5
B) 2,5
C) 2,7
D) 2,75
E) 3
Resposta:
(OBM 2006 – 1ª Fase – Nível 1)
Em um tanque há 4000 bolinhas de pingue-pongue. Um menino começou a retirar as bolinhas, uma por uma, com velocidade constante, quando eram 10h. Após 6 horas, havia no tanque 3520 bolinhas. Se o menino continuasse no mesmo ritmo, quando o tanque ficaria com 2000 bolinhas?
A) às 11h do dia seguinte
B) às 23h do mesmo dia
C) às 4h do dia seguinte
D) às 7h do dia seguinte
E) às 9h do dia seguinte
Resposta:
Em 6h de trabalho foram retiradas![clip_image002[17] clip_image002[17]](https://lh4.ggpht.com/_M-ySlxNhWc8/TcYsvr7baJI/AAAAAAAAAo8/k1u1mBfJ4xk/clip_image002%5B17%5D_thumb.gif?imgmax=800) bolinhas e como a velocidade de retirada é constante, saem
bolinhas e como a velocidade de retirada é constante, saem 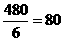 bolinhas por hora.
bolinhas por hora.
Para que 2000 bolinhas saiam do tanque são necessárias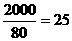 horas.
horas.
Portanto, o tanque ficou com 2000 bolinhas às 11h do dia seguinte.
Resposta correta letra A.
(OBM 2007 – 1ª Fase – Nível 1)
A soma de todos os números positivos ímpares até 2007 menos a soma de todos os números positivos pares até 2007 é igual a:
A) 1003
B) 1004
C) 2005
D) 2006
E) 2007
Resposta:
A soma de todos os números positivos ímpares até 2007 menos a soma dos números positivos pares até 2007 é (1 – 2) + (3 – 4) + (5 – 6) + ... + (2005 – 2006) + 2007 = –1003 + 2007 = 1004.
Resposta correta letra B.
Referência: www.obm.org.br e http://professoraju-mat.blogspot.com/
Um troféu formado por cinco recipientes cúbicos foi construído da seguinte maneira: sob o cubo de lado 10 cm foi soldado o cubo de lado 20 cm, sob este foi soldado o cubo de lado 30 cm, e assim por diante. Toda a superfície externa desse troféu deverá ser coberta com um certo tipo de revestimento. Quantos metros quadrados desse revestimento serão necessários?

A) 1,5
B) 2,5
C) 2,7
D) 2,75
E) 3
Resposta:
Juntando-se as partes das faces superiores dos cubos, obtemos uma face do cubo maior, de aresta 50 cm. A face inferior do cubo também é revestida. As quatro faces laterais dos cinco cubos deverão ser revestidas. Portanto, a área total é igual a
Resposta correta letra C.(OBM 2006 – 1ª Fase – Nível 1)
Em um tanque há 4000 bolinhas de pingue-pongue. Um menino começou a retirar as bolinhas, uma por uma, com velocidade constante, quando eram 10h. Após 6 horas, havia no tanque 3520 bolinhas. Se o menino continuasse no mesmo ritmo, quando o tanque ficaria com 2000 bolinhas?
A) às 11h do dia seguinte
B) às 23h do mesmo dia
C) às 4h do dia seguinte
D) às 7h do dia seguinte
E) às 9h do dia seguinte
Resposta:
Em 6h de trabalho foram retiradas
Para que 2000 bolinhas saiam do tanque são necessárias
Portanto, o tanque ficou com 2000 bolinhas às 11h do dia seguinte.
Resposta correta letra A.
(OBM 2007 – 1ª Fase – Nível 1)
A soma de todos os números positivos ímpares até 2007 menos a soma de todos os números positivos pares até 2007 é igual a:
A) 1003
B) 1004
C) 2005
D) 2006
E) 2007
Resposta:
A soma de todos os números positivos ímpares até 2007 menos a soma dos números positivos pares até 2007 é (1 – 2) + (3 – 4) + (5 – 6) + ... + (2005 – 2006) + 2007 = –1003 + 2007 = 1004.
Resposta correta letra B.
Referência: www.obm.org.br e http://professoraju-mat.blogspot.com/
Comentários
Postar um comentário