Os sólidos de Platão também são denominados de poliedros, pois são formados por faces, arestas e vértices. As faces são constituídas por seções de planos, considerando que entre duas faces temos as arestas, as quais possuem em suas extremidades os vértices.
Platão foi um filósofo grego, que viveu entre os séculos V e IV a.C., e estabeleceu importantes propriedades em alguns poliedros. Os poliedros de Platão possuem características próprias e se enquadram nas seguintes condições:
O número de arestas é igual em todas as faces;
Os ângulos poliédricos possuem o mesmo número de arestas;
Nos sólidos considerados poliedros de Platão vale a relação de Euler (V – A + F = 2) onde V = vértices, A = arestas e F = faces.
O prisma a seguir pode ser considerado um Poliedro da Platão, pois se encaixa nas condições descritas anteriormente.
Platão foi um filósofo grego, que viveu entre os séculos V e IV a.C., e estabeleceu importantes propriedades em alguns poliedros. Os poliedros de Platão possuem características próprias e se enquadram nas seguintes condições:
O número de arestas é igual em todas as faces;
Os ângulos poliédricos possuem o mesmo número de arestas;
Nos sólidos considerados poliedros de Platão vale a relação de Euler (V – A + F = 2) onde V = vértices, A = arestas e F = faces.
O prisma a seguir pode ser considerado um Poliedro da Platão, pois se encaixa nas condições descritas anteriormente.

As seis faces do sólido são quadriláteros, isto é, são formadas por quatro arestas.
Os ângulos são triédricos, pois todos são formados por três arestas.
A relação de Euler pode ser aplicada, observe:
O sólido possui oito vértices, seis faces e 12 arestas:
V – A + F = 2
8 – 12 + 6 = 2
14 – 12 = 2
2 = 2 (verdadeiro)
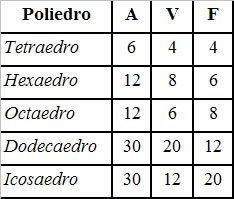
Os poliedros de Platão são classificados em cinco classes de acordo com a tabela a seguir:
Platão estabeleceu algumas relações entre as classes de poliedros e a construção do Universo. Ele associou os poliedros cubo, icosaedro, tetraedro e octaedro, respectivamente, aos elementos terra, água, fogo e ar; e o dodecaedro foi associado ao universo. Conheça os poliedros de Platão:
Os ângulos são triédricos, pois todos são formados por três arestas.
A relação de Euler pode ser aplicada, observe:
O sólido possui oito vértices, seis faces e 12 arestas:
V – A + F = 2
8 – 12 + 6 = 2
14 – 12 = 2
2 = 2 (verdadeiro)
Os poliedros de Platão são classificados em cinco classes de acordo com a tabela a seguir:

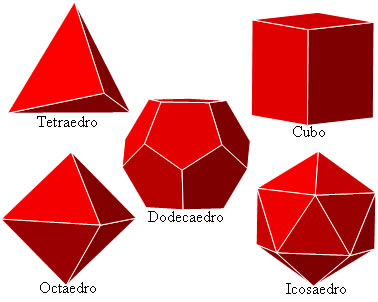
Platão estabeleceu algumas relações entre as classes de poliedros e a construção do Universo. Ele associou os poliedros cubo, icosaedro, tetraedro e octaedro, respectivamente, aos elementos terra, água, fogo e ar; e o dodecaedro foi associado ao universo. Conheça os poliedros de Platão:
Graduado em Matemática
Olá Antonio, cheguei aqui através dos Educadores Multiplicadores. Confesso que não gosto de matemática, mas vim prestigiar seu trabalho. Parabéns! ♥
ResponderExcluirAbraços, Genis
http://redeeducacaoemfoco.blogspot.com.br/
http://blogdagenis.blogspot.com.br/
http://mamaegenis.blogspot.com.br/